Approach to Weekly No. 24

Many people have sent me mail saying that the only approach to Weekly No. 24 is trial and error. Given the volume of mail I am posting the initial approach to the puzzle.

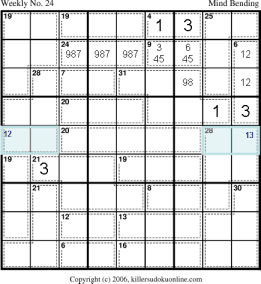
Start by using the rule of 45 on the left 2 columns, yielding: a 3 in r4c2 a 1 in r8c6 The unique sum in the 4-cage combined with the unique sum in the 6-cage yield a 3 in r9c7 a 1 in r9c6 a 3 in r6c9 and the remainder of the 6-cage (1+2) in r7c9 and r8c9. Fill in the unique sum of the 24-cage in row 8. The only possibilities for the 9-cage on row 8 are now 4+5 and 3+6. Now use rule-of-45 on bottom 5 rows to determine the value of the 2 cells (in blue) at the top of the 28-cage on the right of the puzzle. From this figure out the value of the 2 cells at the bottom of the 28-cage on the left, also marked in blue.
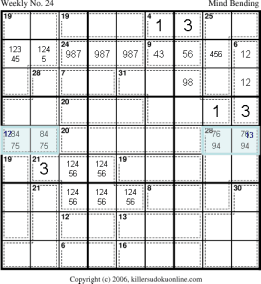
The only possible compatible sums in the two blue cages are 8+4 and 7+5 on the left and 7+6 and 9+4 on the right. The only possible sum in the 21-cage on rows three and four is 3+1+2+4+5+6. From the rule of 45 on the upper right nonet we can see that the leftmost 3 column must sum to 17. This means that r7c7 must be 8 or 9. (This also means that r8c7 cannot be a 4.) Rule of necessity allows us to determine that r8c8 must be 456. Thus, the two rightmost cells of row eight are 12345 and 1245 respectively.
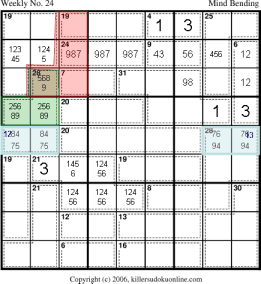
The upper part of 28-cage (in green) must sum to 16. We know that this sum cannot contain either a 3 or a 1. It cannot contain a 3 due to r4c2. It cannot contain a 1 due to the 1 in r6c8 and the fact that the red region must sum to 26 (due to the rule of 45). The red region has 4 cells and there is no 4-cell sum totaling 26 with a 1 in it. We also know that the sum cannot contain both (7 and 8), or (4 and 5), or (8 and 5), or (7 and 4). If it contained any one of these pairs then it would be impossible to fill in the blue part of the 28-cage. This leaves 259 and 268 as the only possible sums for the upper part of the 28-cage. Finally, we know that the 2 must be in r6. If the 2 was in r7c2, this would require the red region to be composed of 9872, however, this would mean that r7c3 in the 7-cage would have a value greater than 6; which is impossible.
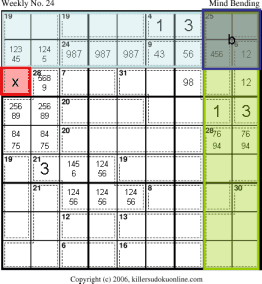
Now, one can use a form of the overlap rule (first proposed by Jean-Christophe Godart) to gather information about the upper right and upper left nonets. In this case, we add the cages contained in the blue and green region to obtain 165. From simple math we can see that region b (in dark blue) is counted once by adding the sum of the cages and counted twice if we just add up the two rows and two columns. That is: 165-x+b = 180. Where 165 is the sum of the cages, x is the extra cell included in the sum of the cages which is not included in the blue rows, b is the area being counted twice by summing up the individual rows and columns, and 180 is the sum of the rows and columns. So, b=15+x. Since the minimum b can be is 17 (4+1+7+5) and the maximum is 24 (6+2+9+7) we can see that x must be between 2 and 9. If you inspect r7 this means that the only cell that could contain a 1 is r7c9.
The rule of 45 now allows us to deduce that x+y = 12. We can now determine that r7c2 cannot be 5 as the 7-cage on r7 must be either 5+2 or 3+4. However, if r7c2 is a 5, then x+y must use either the 3 or the 4. Now we can inspect the 20-cage on r6. Due to the 3 in r6c9, the only valid sums are 875, 974, and 965. However, 875 is not legal as: r6c3 cannot be an 8. If r6c3=8, then r7c2=8 (by rule-of-necessity on the 28-cage) which means that r7c7 must be a 9. But then there is no place for a 9 in r6. r6c3 cannot be either 5 or 7. If either was the case then the 28-cage would be impossible.
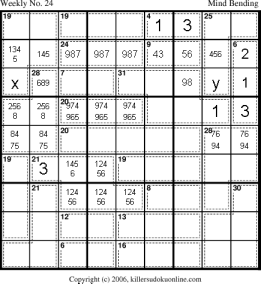We can eliminate the possibility of 259 in the upper part of the 28-cage because a 25 in r6c12 would require 974 in the 20-cage on r6, leaving 68 in r6c67. However, the 9 in r7c2 makes r7c7 an 8, so the 31-cage would have two 8s. This in turn allows us to fix the sum of r5c12 to be 7+5. We can then eliminate the 7 and 5 from the rest of the cells in this nonet. We can also fill in the possible values for the rest of r5.
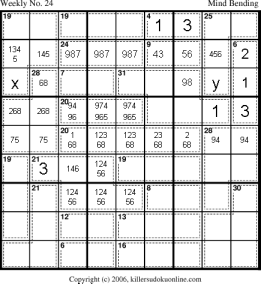We can now eliminate the 8 in r7c2 as it makes the 31-cage impossible. If r7c2 is an 8, then r7c567 must be 6+9+(3 or 4). But, r6c678 can only be 5+8+1; which cannot possibly sum to 31.
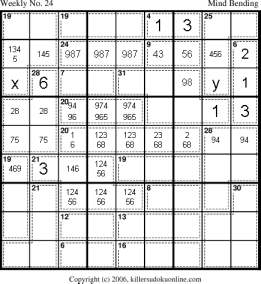Rule-of-necessity makes r6c67 = 65 or 74. Thus red region must equal 19. The only valid sums for the red region are 982, 973, and 874. This mean that r7c56 has to have one of 987. Using the Rule-of-K in the top middle nonet allows us to eliminate all uses of 987 outside of the 24-cage on r8 and the red region. Thus the 19-cage on r9 must be 964 or 865. rule-of-necessity requires a 2 in r9c12. The 7-cage on r7 is thus 5+2, 3+4, or 4+3.
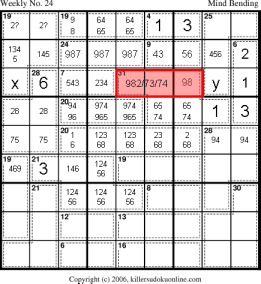Rule-of-necessity make the 19-cage on r9 equal 865. (Since no other 5 is available in the top middle nonet.) The red region in the upper left nonet must sum to 26 by the rule-of-45. Thus, r78c3 must sum to 12. This eliminates the 4 from r7c3.
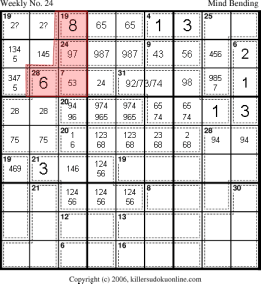In order to make progress we now need some information from the lower part of the puzzle. The first thing to look for is the most constrained cage. This would be the 30-cage in the lower right. It cannot contain either a 1 or a 4. (It cannot have a 4, since the 28-cage above it has a 4 and there is not 4 in r789c7. Thus, c89 already have their fours.) Every sum that makes 30 without a 1 or 4 has a 9! Thus, r789c89 cannot have a 9! This means r7c7 is a 9. There is now a lot of obvious progress that can be made.
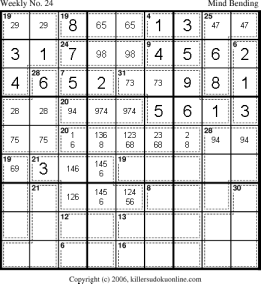The 19-cage in c1, only has one possible sum: 658. The 58 in r23c1 allows us to fix the rest of the cells in the top left nonets. The 6 in r4c1 also clears up column 3 in this nonet. This leaves only 236 for r123c3. However, due to the values of the cages we can immediately place them. At this point, the rest of the puzzle falls into place.
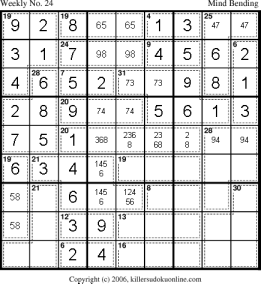